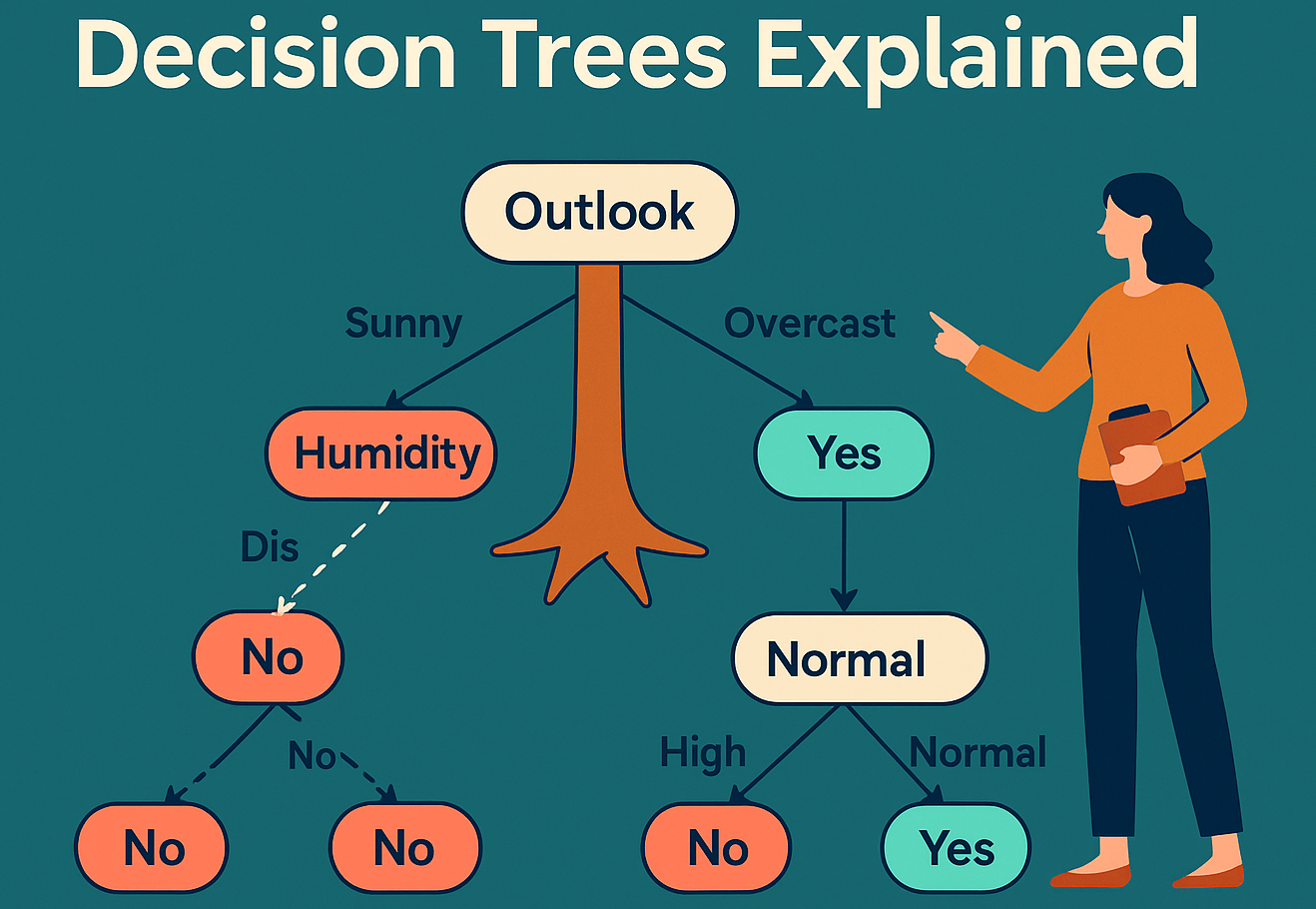
📈 What is Linear Regression?

Linear regression is one of the most fundamental algorithms in machine learning and statistics. It’s used to model the relationship between a dependent variable (target) and one or more independent variables (features).

In simple linear regression, we draw a straight line that best fits the data points.

🧠 When to Use Linear Regression?

• When the relationship between input and output appears linear
• For predicting continuous values (e.g., price, temperature, salary)
• When interpretability is important (easy to explain coefficients)

🧮 The Linear Equation

The basic equation for linear regression is:

y = mx + b

Where:

• y = predicted value
• x = input feature
• m = slope (coefficient)
• b = intercept (bias)

In multiple linear regression (more than one feature), it becomes:

y = b + m1*x1 + m2*x2 + ... + mn*xn

💻 Python Example: Predicting House Prices

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Sample dataset
data = {
    'Size': [1000, 1500, 1800, 2400, 3000],
    'Price': [200000, 250000, 280000, 310000, 370000]
}
df = pd.DataFrame(data)

# Features and target
X = df[['Size']]  # input
y = df['Price']   # output

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Model
model = LinearRegression()
model.fit(X_train, y_train)

# Prediction
predictions = model.predict(X_test)
print("Predicted prices:", predictions)
print("Mean Squared Error:", mean_squared_error(y_test, predictions))

📊 Visualization Tip

To visualize the regression line:

import matplotlib.pyplot as plt

plt.scatter(X, y, color='blue')  # actual data
plt.plot(X, model.predict(X), color='red')  # regression line
plt.xlabel("Size (sq ft)")
plt.ylabel("Price ($)")
plt.title("Linear Regression: House Prices")
plt.show()

✅ Strengths

• Simple and fast
• Easy to interpret
• Works well with linearly separable data

❌ Limitations

• Struggles with non-linear relationships
• Sensitive to outliers
• Assumes homoscedasticity and normal distribution of errors

🧭 Conclusion

Linear regression is a great starting point for any regression task. It helps you understand your data, find patterns, and build predictive models. With just a few lines of Python code, you can apply it to real-world datasets and begin your machine learning journey.

Ready to try it? Grab a dataset and draw your first regression line!